Python 源码学习(2):int 类型
Python 中的标准数据类型有六种,分别是 number, string, list, tuple, set, dictionary,前文已经阐述过它们的对象类型都是继承了 PyBaseObject_Type 类型的 PyType_Type 类型的实例对象,本文则主要探究 Python 中 int 类型的实现。
不同于 C 和 C++ 中的 int 类型,Python 中的 int 类型最大的特点是它一般是不会溢出的,对比用 C 和 Python 分别输出两个一百万相乘的结果:
>>> x = 10000000000
>>> print(x)
10000000000
在 C 语言中会发生溢出:
printf("%d\n", 1000000 * 1000000);
printf("%u\n", 1000000 * 1000000);
-727379968
3567587328
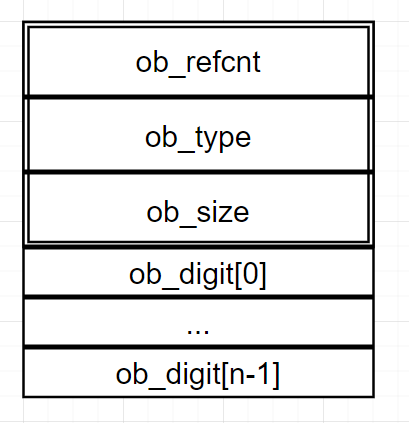
1 int 类型在内存中的存储方式
1.1 内存结构
Python 中的 int 整数类型实际上是一个名为 PyLongObject 的结构体,定义在 longintrepr.h 文件中:
// Include/object.h
#define PyObject_VAR_HEAD PyVarObject ob_base;
// Objects/longobject.h
#if PYLONG_BITS_IN_DIGIT == 30
typedef uint32_t digit;
// ...
#elif PYLONG_BITS_IN_DIGIT == 15
typedef unsigned short digit;
// ...
#endif
typedef struct _longobject PyLongObject; /* Revealed in longintrepr.h */
// Include/longintrepr.h
struct _longobject {
PyObject_VAR_HEAD
digit ob_digit[1];
};
它由两部分组成,分别是:
一个变长对象
PyVarObject ob_base,其中包括引用计数Py_ssize_t ob_refcnt、类型指针PyTypeObject *ob_type、变长部分的长度Py_ssize_t ob_size,表明PyLongObject也是一个变长对象;一个
digit类型的数组ob_digit,用于存储整数值,数组长度默认为 1,在初始化时如果长度不够则会被扩大;digit是一个被PYLONG_BITS_IN_DIGIT宏控制的类型,在编译 Python 解释器时可以通过修改这个宏来指定其类型;如果没有指定PYLONG_BITS_IN_DIGIT宏的值,则默认会根据操作系统的类型来决定,当指针占用 8 字节以上空间时(64 位以上操作系统),PYLONG_BITS_IN_DIGIT = 30,digit即为uint32_t,否则PYLONG_BITS_IN_DIGIT = 15,digit则是unsigned short:
#ifndef PYLONG_BITS_IN_DIGIT #if SIZEOF_VOID_P >= 8 #define PYLONG_BITS_IN_DIGIT 30 #else #define PYLONG_BITS_IN_DIGIT 15 #endif #endif
`PyLongObject` 的内存结构大致如图:
### 1.2 数据表示
在 `ob_digit` 数组中,数据的表示遵循两个原则:
1. `ob_size` 的绝对值表示 `ob_digit` 数组的长度,`ob_size = 0` 表示 `PyLongObject` 的数值等于 0;数据的正负由 `ob_size` 的正负来标识,`ob_size > 0` 表示 `PyLongObject > 0`,`ob_size < 0` 表示 `PyLongObject < 0`;
2. `ob_digit` 数组的每一个元素都是一个最大为 `2^30`(假设 `PYLONG_BITS_IN_DIGIT == 30`)的整数,如果整数超过了这个值,则会清零并使其后一位自增 1,假设 `ob_size = n`,那么数据的绝对值则等于 `ob_digit[0] + ob_digit[1] * 2^30 + ob_digit[2] * 2^60 + ... + ob_digit[n-1] * 2^(30 * (n-1))`;
例如对于整数 4294967297,可以被表示为 `1 + 4 * 2^30`,因此其 `ob_size = 2`, `ob_digit[0] = 1`, `ob_digit[1] = 4`,其内存结构大致如图:

通过这种大数存储方式,Python 从语言层面解决了 `2^(30*2147483648) - 1` 以下(`ob_size` 的类型 `Py_ssize_t` 是通过 `typedef long int Py_ssize_t` 定义的)的大数的溢出问题。
### 1.3 创建对象
在 Python 中, `PyLongObject` 对象一般是通过 `_PyLong_New` 函数创建出来的:
```cpp
/* Allocate a new int object with size digits.
Return NULL and set exception if we run out of memory. */
#define MAX_LONG_DIGITS \
((PY_SSIZE_T_MAX - offsetof(PyLongObject, ob_digit))/sizeof(digit))
PyLongObject *
_PyLong_New(Py_ssize_t size)
{
PyLongObject *result;
/* Number of bytes needed is: offsetof(PyLongObject, ob_digit) +
sizeof(digit)*size. Previous incarnations of this code used
sizeof(PyVarObject) instead of the offsetof, but this risks being
incorrect in the presence of padding between the PyVarObject header
and the digits. */
if (size > (Py_ssize_t)MAX_LONG_DIGITS) {
PyErr_SetString(PyExc_OverflowError,
"too many digits in integer");
return NULL;
}
result = PyObject_MALLOC(offsetof(PyLongObject, ob_digit) +
size*sizeof(digit));
if (!result) {
PyErr_NoMemory();
return NULL;
}
_PyObject_InitVar((PyVarObject*)result, &PyLong_Type, size);
return result;
}
这个函数非常简单,主要是做了两件事:
- 内存分配前后的检查,包括参数
size不能超过MAX_LONG_DIGITS,也就是说PyLongObject所表示的整数大小不能超过2^(30*2147483648) - 1,以及生成使用malloc分配内存失败后的报错信息; - 为
PyLongObject对象申请内存,其大小分为两部分,第一部分是PyVarObject在内存对齐后所占用的空间,即offsetof(PyLongObject, ob_digit);第二部分是ob_digit数组所占用的空间,其中参数size是ob_digit数组的长度。
1.4 数据转化
每一个 PyLongObject 对象都拥有不同的内存地址,我们可以通过 Python 中的 id 函数来查看一个变量的标识,这个标识会因内存地址的不同而改变:
for i in range(5):
print(id(i))
$ python3 main.py
139748219328384
139748219328416
139748219328448
139748219328480
139748219328512
可以看出 0 到 4 这 5 个数的标识里每两个都相差了 32,刚好符合每一个 PyLongObject 对象所占用的空间 32 字节,而不是 C 语言里一个 long 类型变量通常所占用的 4 字节或 8 字节,这是因为所有原始的数据都会被转化为 PyLongObject 对象。
数据转化的方法有很多,以 PyLong_FromLong 为例,它会将一个 long 类型的整数转化为 PyLongObject 对象:
// Objects/longobject.c
/* interpreter state */
#define _PY_NSMALLPOSINTS 257
#define _PY_NSMALLNEGINTS 5
#define NSMALLNEGINTS _PY_NSMALLNEGINTS
#define NSMALLPOSINTS _PY_NSMALLPOSINTS
#define IS_SMALL_INT(ival) (-NSMALLNEGINTS <= (ival) && (ival) < NSMALLPOSINTS)
PyObject *
PyLong_FromLong(long ival)
{
PyLongObject *v;
unsigned long abs_ival;
unsigned long t; /* unsigned so >> doesn't propagate sign bit */
int ndigits = 0;
int sign;
if (IS_SMALL_INT(ival)) {
return get_small_int((sdigit)ival);
}
if (ival < 0) {
/* negate: can't write this as abs_ival = -ival since that
invokes undefined behaviour when ival is LONG_MIN */
abs_ival = 0U-(unsigned long)ival;
sign = -1;
}
else {
abs_ival = (unsigned long)ival;
sign = ival == 0 ? 0 : 1;
}
/* Fast path for single-digit ints */
if (!(abs_ival >> PyLong_SHIFT)) {
v = _PyLong_New(1);
if (v) {
Py_SET_SIZE(v, sign);
v->ob_digit[0] = Py_SAFE_DOWNCAST(
abs_ival, unsigned long, digit);
}
return (PyObject*)v;
}
#if PyLong_SHIFT==15
/* 2 digits */
if (!(abs_ival >> 2*PyLong_SHIFT)) {
v = _PyLong_New(2);
if (v) {
Py_SET_SIZE(v, 2 * sign);
v->ob_digit[0] = Py_SAFE_DOWNCAST(
abs_ival & PyLong_MASK, unsigned long, digit);
v->ob_digit[1] = Py_SAFE_DOWNCAST(
abs_ival >> PyLong_SHIFT, unsigned long, digit);
}
return (PyObject*)v;
}
#endif
/* Larger numbers: loop to determine number of digits */
t = abs_ival;
while (t) {
++ndigits;
t >>= PyLong_SHIFT;
}
v = _PyLong_New(ndigits);
if (v != NULL) {
digit *p = v->ob_digit;
Py_SET_SIZE(v, ndigits * sign);
t = abs_ival;
while (t) {
*p++ = Py_SAFE_DOWNCAST(
t & PyLong_MASK, unsigned long, digit);
t >>= PyLong_SHIFT;
}
}
return (PyObject *)v;
}
虽然看起来比较长,但其实思路非常简单:
- 创建用于存储返回值的指针
PyLongObject *z,保存数据绝对值的变量unsigned long abs_ival, t,标识数组长度的int ndigits和标识数据正负的int sign; - 如果数据范围在 [-5, 257) 内,则通过
get_small_int函数返回结果; - 获取数据的绝对值和正负符号;
- 如果数据绝对值没有超过
ob_digit数组的单个元素所能表示的大小,则通过一个快速路径返回结果; - 对于较大的数据,确定其
ob_digit数组的长度,逐位置入。
可以注意到,第 2 步针对 [-5, 257) 区间内的小整数做了特殊处理,最终在调用到 __PyLong_GetSmallInt_internal 函数时,会通过 tstate->interp->small_ints[index] 缓存数组获取小整数对应的指针对象并将其返回,这里的 small_ints 数组是一个全局变量,一般称为小整数对象池,是针对常用的小整数做的一个优化:
// Objects/longobject.c
static inline PyObject* __PyLong_GetSmallInt_internal(int value)
{
PyThreadState *tstate = _PyThreadState_GET();
#ifdef Py_DEBUG
_Py_EnsureTstateNotNULL(tstate);
#endif
assert(-_PY_NSMALLNEGINTS <= value && value < _PY_NSMALLPOSINTS);
size_t index = _PY_NSMALLNEGINTS + value;
PyObject *obj = (PyObject*)tstate->interp->small_ints[index];
// _PyLong_GetZero() and _PyLong_GetOne() must not be called
// before _PyLong_Init() nor after _PyLong_Fini()
assert(obj != NULL);
return obj;
}
2 数学运算
PyLongObject 的类型对象是 PyLong_Type,PyLong_Type 的成员变量 PyNumberMethods *tp_as_number 由 static PyNumberMethods long_as_number* 结构体指针初始化,其中包含了许多数学运算的函数指针,当我们对 PyLong_Type 进行数学运算时,实际上会调用这些函数:
// Objects/longobject.c
PyTypeObject PyLong_Type = {
// ...
&long_as_number, /* tp_as_number */
// ...
};
static PyNumberMethods long_as_number = {
(binaryfunc)long_add, /*nb_add*/
(binaryfunc)long_sub, /*nb_subtract*/
(binaryfunc)long_mul, /*nb_multiply*/
long_mod, /*nb_remainder*/
long_divmod, /*nb_divmod*/
long_pow, /*nb_power*/
// ...
};
2.1 加法
PyLong_Type 的加法运算对应的函数是 long_add,其实现和相关的宏定义如下:
// Objects/longobject.c
#define CHECK_BINOP(v,w) \
do { \
if (!PyLong_Check(v) || !PyLong_Check(w)) \
Py_RETURN_NOTIMPLEMENTED; \
} while(0)
/* convert a PyLong of size 1, 0 or -1 to an sdigit */
#define MEDIUM_VALUE(x) (assert(-1 <= Py_SIZE(x) && Py_SIZE(x) <= 1), \
Py_SIZE(x) < 0 ? -(sdigit)(x)->ob_digit[0] : \
(Py_SIZE(x) == 0 ? (sdigit)0 : \
(sdigit)(x)->ob_digit[0]))
static PyObject *
long_add(PyLongObject *a, PyLongObject *b)
{
PyLongObject *z;
CHECK_BINOP(a, b);
if (Py_ABS(Py_SIZE(a)) <= 1 && Py_ABS(Py_SIZE(b)) <= 1) {
return PyLong_FromLong(MEDIUM_VALUE(a) + MEDIUM_VALUE(b));
}
if (Py_SIZE(a) < 0) {
if (Py_SIZE(b) < 0) {
z = x_add(a, b);
if (z != NULL) {
/* x_add received at least one multiple-digit int,
and thus z must be a multiple-digit int.
That also means z is not an element of
small_ints, so negating it in-place is safe. */
assert(Py_REFCNT(z) == 1);
Py_SET_SIZE(z, -(Py_SIZE(z)));
}
}
else
z = x_sub(b, a);
}
else {
if (Py_SIZE(b) < 0)
z = x_sub(a, b);
else
z = x_add(a, b);
}
return (PyObject *)z;
}
可以看到它的实现非常简单,主要分为以下几个步骤:
- 创建一个用于存储返回值的指针
PyLongObject *z; - 检查两个参数是否都是
PyLongObject类型的指针CHECK_BINOP(a, b); - 如果两个参数都满足
ob_size <= 1(即绝对值均小于2^30),那么先通过MEDIUM_VALUE获取两个ob_digit[0]的值,并将两数直接相加(一定不会溢出),再通过PyLong_FromLong将这个数包装为一个PyLongObject指针并返回;通常我们进行运算的数都不会太大,因此这里可以利用简化的运算步骤和 CPU 分支预测来提高效率; - 判断两者的正负关系,将问题简化为绝对值加减法,利用辅助函数
x_add和x_sub进行运算并返回结果。
2.2 绝对值加法
绝对值加法函数 x_add 的定义如下:
#if PYLONG_BITS_IN_DIGIT == 30
#define PyLong_SHIFT 30
// ...
#endif
#define PyLong_BASE ((digit)1 << PyLong_SHIFT)
#define PyLong_MASK ((digit)(PyLong_BASE - 1))
/* Add the absolute values of two integers. */
static PyLongObject *
x_add(PyLongObject *a, PyLongObject *b)
{
Py_ssize_t size_a = Py_ABS(Py_SIZE(a)), size_b = Py_ABS(Py_SIZE(b));
PyLongObject *z;
Py_ssize_t i;
digit carry = 0;
/* Ensure a is the larger of the two: */
if (size_a < size_b) {
{ PyLongObject *temp = a; a = b; b = temp; }
{ Py_ssize_t size_temp = size_a;
size_a = size_b;
size_b = size_temp; }
}
z = _PyLong_New(size_a+1);
if (z == NULL)
return NULL;
for (i = 0; i < size_b; ++i) {
carry += a->ob_digit[i] + b->ob_digit[i];
z->ob_digit[i] = carry & PyLong_MASK;
carry >>= PyLong_SHIFT;
}
for (; i < size_a; ++i) {
carry += a->ob_digit[i];
z->ob_digit[i] = carry & PyLong_MASK;
carry >>= PyLong_SHIFT;
}
z->ob_digit[i] = carry;
return long_normalize(z);
}
其步骤大致分为以下几步:
- 获取两个参数的
ob_size的绝对值,创建存储返回值的指针PyLongObject *z, - 如果
a->ob_size < b->ob_size则交换两者,保证 a 的值较大; - 将 z 的
ob_size设置为size_a + 1,保证不会溢出; - 以
i = 0为下标,从小到大依次对两数的每一位进行相加操作,将没有超过2^30的部分存储在z->ob_digit[i]中,超过的部分进位保存在carry中;这里充分利用了两个小于2^30的数相加不会溢出的特性;如果size_a > size_b还需要将a->ob_digit多余的部分按照相同的方法置入z->ob_digit里; - 得到的结果
z中,其ob_digit的最后一个元素可能等于 0,因此通过long_normalize函数将其转换为符合PyLongObject定义的格式返回。
整个过程可以抽象为类似 2^30 进制的加法,和十进制加法的过程几乎完全一样,只不过是把十进制每一位的数字换成了一个最大值为 2^30 的数字,每逢 2^30 进一位;举个例,假设有 a->ob_digit = {4, 5, 6}, b->ob_digit = {1073741823, 1073741823},那么整个加法的步骤为:
v->ob_digit[0] = (4 + 1073741823) % 1073741824 = 3,carry = 1;v->ob_digit[1] = (5 + 1073741823 + 1) % 1073741824 = 5,carry = 1;v->ob_digit[2] = (6 + 1) % 1073741824 = 7,carry = 0;v->ob_digit[3] = 0;
结果即 v->ob_digit = {3, 5, 7, 0},最后一个元素 0 需要通过 long_normalize 函数去掉。
2.3 绝对值减法
绝对值减法的实现如下:
/* Subtract the absolute values of two integers. */
static PyLongObject *
x_sub(PyLongObject *a, PyLongObject *b)
{
Py_ssize_t size_a = Py_ABS(Py_SIZE(a)), size_b = Py_ABS(Py_SIZE(b));
PyLongObject *z;
Py_ssize_t i;
int sign = 1;
digit borrow = 0;
/* Ensure a is the larger of the two: */
if (size_a < size_b) {
sign = -1;
{ PyLongObject *temp = a; a = b; b = temp; }
{ Py_ssize_t size_temp = size_a;
size_a = size_b;
size_b = size_temp; }
}
else if (size_a == size_b) {
/* Find highest digit where a and b differ: */
i = size_a;
while (--i >= 0 && a->ob_digit[i] == b->ob_digit[i])
;
if (i < 0)
return (PyLongObject *)PyLong_FromLong(0);
if (a->ob_digit[i] < b->ob_digit[i]) {
sign = -1;
{ PyLongObject *temp = a; a = b; b = temp; }
}
size_a = size_b = i+1;
}
z = _PyLong_New(size_a);
if (z == NULL)
return NULL;
for (i = 0; i < size_b; ++i) {
/* The following assumes unsigned arithmetic
works module 2**N for some N>PyLong_SHIFT. */
borrow = a->ob_digit[i] - b->ob_digit[i] - borrow;
z->ob_digit[i] = borrow & PyLong_MASK;
borrow >>= PyLong_SHIFT;
borrow &= 1; /* Keep only one sign bit */
}
for (; i < size_a; ++i) {
borrow = a->ob_digit[i] - borrow;
z->ob_digit[i] = borrow & PyLong_MASK;
borrow >>= PyLong_SHIFT;
borrow &= 1; /* Keep only one sign bit */
}
assert(borrow == 0);
if (sign < 0) {
Py_SET_SIZE(z, -Py_SIZE(z));
}
return maybe_small_long(long_normalize(z));
}
其步骤和绝对值加法类似,大致分为以下几步:
- 获取两个参数的
ob_size的绝对值,创建存储返回值的指针PyLongObject *z, - 如果
a->ob_size < b->ob_size则交换两者,保证 a 的值较大,并用sign记录运算结果为负;如果a->ob_size == b->ob_size则从最高位依次往低位找到第一次出现a->ob_digit[i] != b->ob_digit[i]的位置,比较a->ob_digit[i]和b->ob_digit[i],并决定是否交换两者以及sign的值; - 将 z 的
ob_size设置为size_a; - 以
i = 0为下标,从小到大依次对两数的每一位进行相减操作,如果被减数a->ob_digit[i]小于减数b->ob_digit[i]则要向高位a->ob_digit[i + 1]借 1;在十进制的减法中向高位借到的数是 10,这里向digit数组的高位借到的则是2^30;但digit是通过typedef uint32_t digit定义出来,通过公式borrow = a->ob_digit[i] - b->ob_digit[i] - borrow实际上得到的是2^32 + a->ob_digit[i] - b->ob_digit[i],所以还需要与PyLong_MASK做&操作,取后 30 位,便能得到借位相减后的结果,再将结果存储在z->ob_digit[i]中;借位部分borrow向右位移 30 位后还剩 2 位,只需要将其与 1 进行&操作即可知道此次减法运算是否有借位;如果size_a > size_b还需要将a->ob_digit多余的部分按照相同的方法置入z->ob_digit里; - 得到的结果
z中,其ob_digit的最后一个元素可能等于 0,因此通过long_normalize函数将其转换为符合PyLongObject定义的格式返回。
可以看到这里的步骤也跟十进制减法几乎完全相同,都跟 NOIP 入门的大数加减法加法思路相同。