负载均衡和一致性哈希
反向代理 reverse proxy 是指以代理服务器来接收由客户端发送来的请求,并通过一定的策略将其转变发给实际处理请求的后端服务器;主要应用于负载均衡、动态缓存、安全认证、内网穿透、SSL 加密等;而负载均衡 load balancing 是指在多个 slot(槽,一般是某种计算资源)中分配负载,以优化资源利用率和避免单点故障问题的方法,是高可用性分布式系统的必备中间件;常用的开源 load balancer 有 nginx,LVS,Haproxy 等;负载均衡可以视为反向代理的一种应用,负载均衡的方法大致可以分为传统负载均衡算法和哈希算法两种,本文简单地总结了这些算法的原理。
1 传统负载均衡算法
- 随机 random:将 key 随机分配到某一个 slot 上,根据概率论可知,吞吐量越大,随机算法的效果越好;
- 加权随机 weighted random:为每一个 slot 分配一个权重,在随机的时候考虑权重的影响;可以通过在所有 slot 的权重总和中随机出一个数字 k,找到 k 所在的 slot 位置来实现;
- 轮询 round robin:按顺序依次将 key 分配给每一个 slot;
- 加权轮询 weighted round robin:为每一个 slot 分配一个权重,在按序分配时为权重更高的 slot 分配更多的 key;
- 平滑加权轮询 smooth weighted round robin:一种能够均匀地分散调度序列的加权轮询方法,分为以下几个步骤:
- 选出当前权重最高的 slot,将 key 分配给它;
- 将选出的 slot 的权重数值减去其初始权重;
- 将所有 slot 的权重数值都加上它们的原始权重;
- 重复以上步骤;
- 最少连接数 least connections:将 key 分配给当前具有最少连接数量的 slot;
2 Mod-N 哈希
在有些场景下,传统负载均衡算法无法满足我们的需求,例如:
- 当我们需要充分利用到 slot 的缓存,在任何时候都希望将同一个 key 映射到固定的 slot 上,而不是让其被任意地分配到一个负载较低的 slot 上;
- 当我们希望把数据分配到一些具有键值存储功能(可以是 memcache, redis, mysql 等)的 slot 上进行有状态服务,而又不使用一个全局的数据库;
对于以上两个问题,我们可以先使用哈希函数(如 md5, sha1 等,需要保证哈希后的分布平均)将 key 映射为一个 uint32 的值(key 本身可能是一个字符串或其他值),再用该值对 N(slot 的数量)进行取模运算来映射出一个值, 即 value = hash(key) mod n,这种方法可以称为 Mod-N 哈希;这里做了两次哈希,第一次是对 key 做映射,第二次是进行取模运算。
一般来说好的哈希函数应该满足一些条件:
- 从哈希值不可反向推导出 key;
- 发生哈希冲突的概率尽可能小;
- 效率高;
哈希冲突/碰撞 Hash Collision
当我们把较大的值空间映射到较小的值空间时,冲突是不可避免的;如果两个 key 通过哈希方法被映射为了同一个值,那么就称为发生了 hash collision,一般来说其解决方案有:
(1) 单链表法 separate chaining
也称作 open hashing;对于每一个通过哈希方法映射出的值,我们将其作为一个 bucket;当有 key 被映射到 bucket 上时,如果 bucket 为空,则为其新分配一个链表节点,否则遍历这个链表,在这个链表的尾部为其分配新的链表节点;

(2) 开放寻址法 open addressing
也称作 closed hashing;主要思路是通过搜索哈希表中的其他空的 slot(探测序列 probe sequence)来进行 key 的插入,进行查找时应该采用与插入时相同的线性探测规则;获取 probe sequence 的方法一般有:
线性探测 linear probing:查找哈希表中离冲突位置最近的空的 slot,即
value = (hash(key) + k) mod n, k = 1, 2, 3, 4...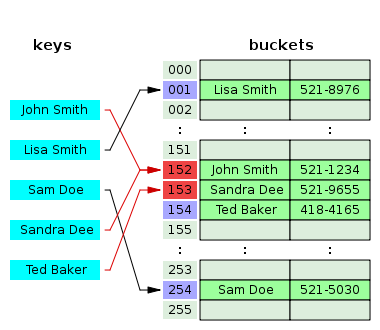
二次探测 quadratic probing:对哈希结果添加一个二次多项式直到找到一个空的 slot,即
value = (hash(key) + k^2) mod n, k^2 = 1, 4, 9, 16...双重哈希 double hashing:借助另一个哈希函数 hash’ 的结果,作为偏移量获取值,即
value = hash'(key) mod n;
3 一致性哈希 Consistent Hashing
在数据量较大的场景下,假设我们因为某些原因需要将原本的 n 个 slot 扩容为 m 个 slot,如果仍然使用 Mod-N 哈希,将会有 n/m 份缓存不能正确命中,从而产生大量的数据库请求,可能导致缓存雪崩。
对于传统的哈希映射,添加或者删除一个 slot,会造成哈希表的全量重新映射;而**一致性哈希**的目的是达成增量式的重新映射,即当 slot 的数量发生变化时,降低重新映射的数量,尽量最小化重新映射(minimum disruption)。
一致性哈希算法的设计关键有 4 点:
- 平衡性 balance:所有的 key 能被均匀地映射到各个 slot 上;
- 单调性 monotonicity:增加新的 slot 后,原有的 key 应该被映射到原有的 slot,或新的 slot 上,而不是其他旧的 slot ;
- 分散 spread:服务扩容或者缩容时,尽量减少数据的迁移;
- 负载 load:尽量降低 slot 的负载;
3.1 Ketama
ketama 算法是最常用的一种一致性哈希算法,也叫做哈希环法(hash ring), 被广泛的应用在数据库,缓存系统和服务框架上,包括但不限于 memcache, redis, dubbo, nginx 等,其步骤是:
- 对于一个 [0, uint32] 的区间,将其首尾相连,形成顺时针的环;
- 对 slot 进行哈希,映射到 [0, uint32] 区间上,并将结果标记到环上;
- 对 key 进行哈希,映射到区间上,沿着环顺时针寻找并将其分配到距其最近的 slot;
举个例子,假设现在有 N0, N1, N2 三个 slot 以及 a, b, c 三个 key,其中 a 会被分配 N1 上,b 和 c 都会被分配到 N2 上;
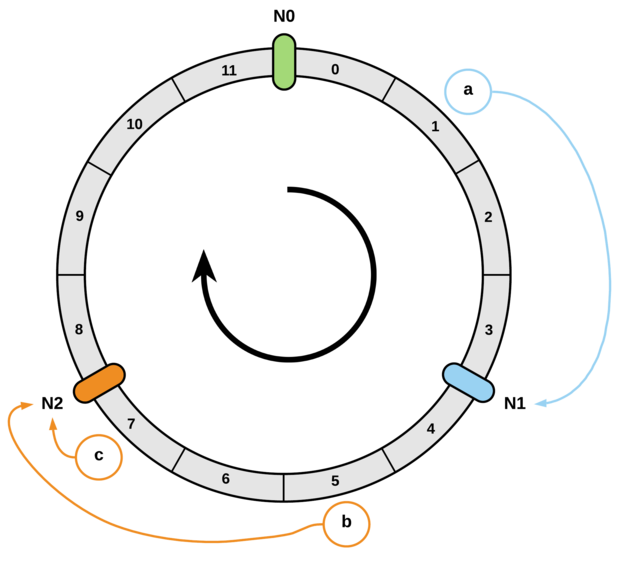
现在我们新增一个 N3 slot,并将其映射到 [a, N1] 之间,那么 a 和所有在 [N0, N3] 之间的 key 都会被重新分配到 N3 这个 slot 上,除此之外的其他所有 key 则不会被重新映射;
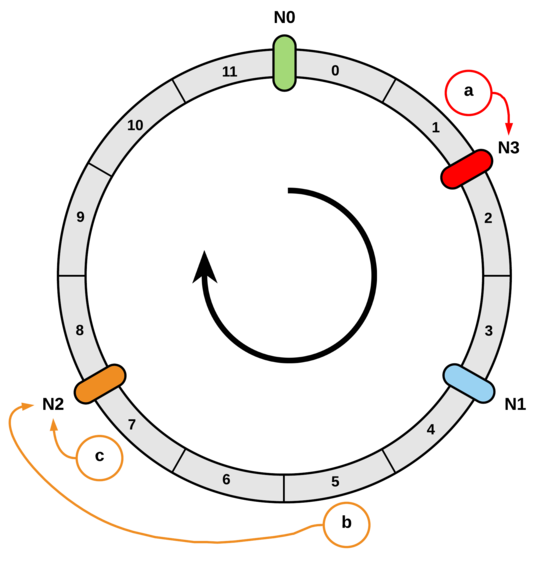
假设我们移除 N2 slot,那么所有在 [N1, N2] 之间的 key 都会被重新映射到 N0 上,除此之外的其他所有 key 则不会被重新映射。
可以发现,ketama 算法达成了在新增或移除 slot 后的增量式重新映射(minimum disruption),不会破坏大多数 key 的映射关系;因为要构造出一个环来存储所有 slot 的 key 被映射到的位置,所以其空间复杂度是 O(n);为了方便地进行查找,可以将环转换成一个有序数组,在其中进行二分查找,时间复杂度是 O(logn)。
虚拟节点
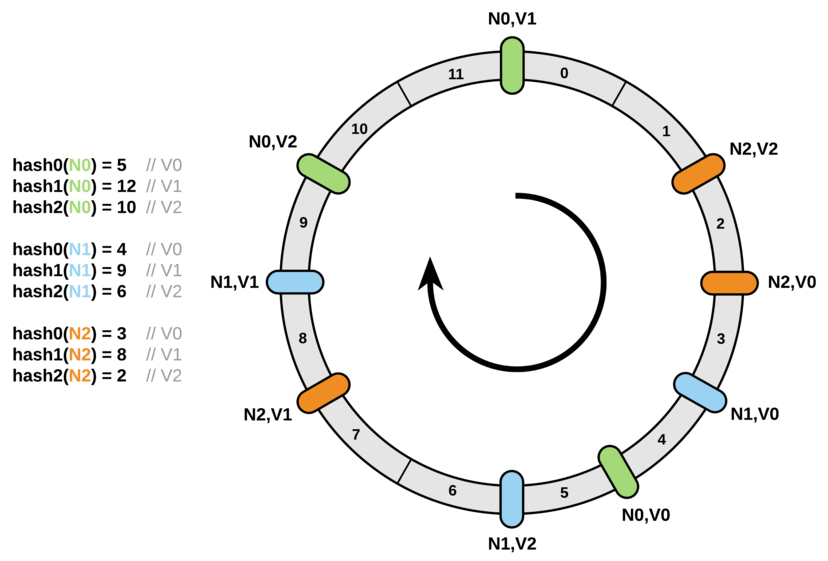
有时候我们可能会对不同的节点赋予不同的权重,也就导致了每个节点的地位不平等,从而不能直接将节点放在环上,解决方案是使用不同数量的虚拟节点(virtual node)来代表实际的节点,一般来说每个虚拟节点代表一个单位节点,虚拟节点数量之和等于实际节点的权重;即使不同节点之间的权重相同,也建议将一个实际节点映射为多个虚拟节点,因为节点越多,它们在环上的分布就越均匀,因此使用虚拟节点还可以降低节点之间的负载差异;假设 N0, N1, N2 三个节点具有相同的权重,那么用虚拟节点代替之后则大致如图:
3.2 Jump Consistent Hashing
Jump Consistent Hashing 跳跃一致性哈希是 Google 发表的一个非常简洁的一致性哈希算法,其主要思路是:
- 假设有 n 个 slot 和 k 个 key,所有的 k 个 key 都被均匀地映射到了这 n 个 slot 上;
- 现在增加 1 个 slot,为了将原有的 k 个 key 均匀地映射到 n + 1 个 slot 上,需要将其中 k / n + 1 个 key 进行重新映射,即每次增加 1 个 slot 都需要重新映射 k / n + 1 个 key;
- 使用**伪随机**的方式(给定一个随机种子,生成一个固定的随机序列)来决定哪 k / n 个 key 需要被重新映射;
这里使用伪随机的含义是,对于每一个 key,我们使用这个 key 来作为随机种子,生成一个固定的随机序列 seq,于是 seq 在其下标为 [1, n] 的区间里的值都是固定的;接下来遍历 seq,在每一次迭代 i 中,如果 seq[i] < 1/i,则将其重新分配到第 i 个 slot 上,否则保持不变;整个过程在给定 key 时就已经确定了。

这样一来就达成了一致性哈希的平衡性和单调性,没有使用额外的内存,所以空间复杂度是 O(1);而因为遍历了 n 个 slot,所以时间复杂度是 O(n),还可以从时间复杂度的角度继续优化;在 seq[i] < 1 / i 这个公式中(即被重新分配这个假设成立),1 / i 会随着 i 的增大而变得越来越小,而 seq[i] 是随机数,因此可以认为公式成立的概率会越来越小,所以我们可以让 i 的步进增大,来减少迭代的次数。
假设当前 key 所在的 slot 是 b,迭代次数是 b + 1 ,下一次迭代某一个 key 会被重新映射的概率是 1 / b + 2(上面思路第 2 点),即其不会被重新分配到新 slot 的概率为 b + 1 / b + 2,再下一次的概率是 b + 2 / b + 3,直到第 j 次的概率是 j - 1 / j,将这些概率相乘得到在这 j - b 次之间 key 不会被重新分配的概率是 b + 1 / j;假设把 seq[i] 用 r = random.next() 来表示,要使得 r < (b + 1) / j(即被重新分配这个假设成立),就必须有 j < (b + 1) / r,那么 key 在步进大于等于 (b + 1) / r 次后一定会被重新分配。

这样一来时间复杂度就减少到了 O(ln(n));但其局限性也很明显,因为只能通过步进的方式来重新映射和分配 slot,导致其只能在尾部增删 slot,否则在中间进行增删的话会导致其后续的 slot 下标和步进关系都发生变化,
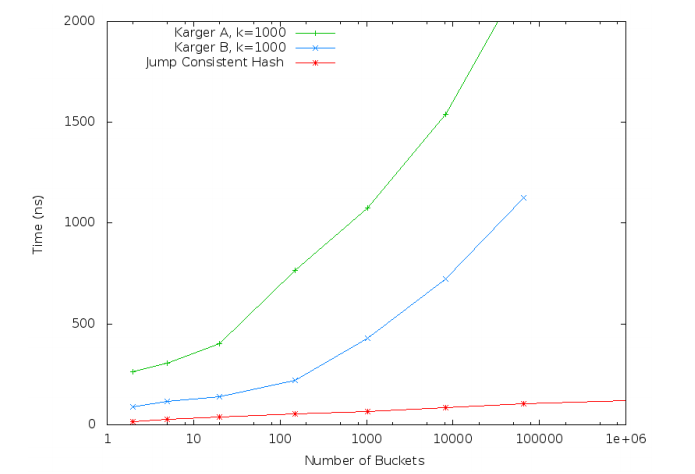
论文中还对比了其与哈希环法的运行时间。
3.3 Maglev Hashing
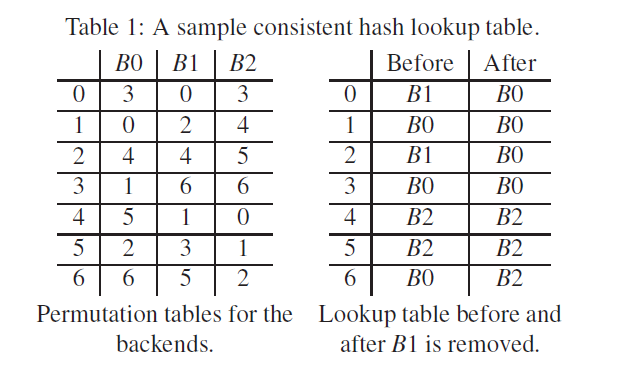
Maglev 是 Google 研发的一个负载均衡组件,使用了其自研的一致性哈希算法 Maglev Hashing,其主要思路是通过维护两个 table 来将 key 映射到 slot 上;一个表是 lookup table 查找表,用于将 key 映射到 slot 上;另一个表是 permutation table 排列表,用于记录一个 slot 在 lookup table 中的位置序列:
对于 n 个 slot 和一个长度为 m 的映射序列(即 permutation table 和 lookup table 的长度),我们希望为每一个下标为 i 的 slot 都计算出一个数量为 m 的排列,计算时需要使用两个不同的哈希函数 h1 和 h2,来计算 offset 和 skip 两个值(这里需要保证每一个 slot 的 name 都不相同):
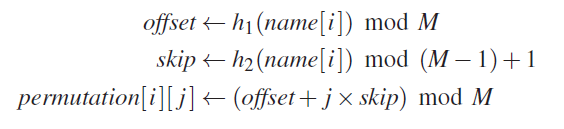
举个例子,假设 n = 3,m = 7,对于下标为 0 的 slot,通过某两个哈希函数计算出来的 offset = 3,skip = 4,为其生成一个长度 m = 7 的 permutation:
permutation[i][0] = (3 + 0 * 4) mod 7 = 3
permutation[i][1] = (3 + 1 * 4) mod 7 = 0
permutation[i][2] = (3 + 2 * 4) mod 7 = 4
permutation[i][3] = (3 + 3 * 4) mod 7 = 1
permutation[i][4] = (3 + 4 * 4) mod 7 = 5
permutation[i][5] = (3 + 5 * 4) mod 7 = 2
permutation[i][6] = (3 + 6 * 4) mod 7 = 6
再加上另外两个计算好 permutation 的下标为 1 和 2 的 slot,对应的 permutation table:
| m | s0 | s1 | s2 |
|---|---|---|---|
| 0 | 3 | 0 | 3 |
| 1 | 0 | 2 | 4 |
| 2 | 4 | 4 | 5 |
| 3 | 1 | 6 | 6 |
| 4 | 5 | 1 | 0 |
| 5 | 2 | 3 | 1 |
| 6 | 6 | 5 | 2 |
现在我们让 3 个 slot 轮流地从其 permutation 中,按顺序选择第一个没有被分配的 key,来填充到之后的 lookup table 中,流程是:
- s0 的 permutation 中的第一个数字 3 没有被分配,选择 3;
- s1 的 permutation 中的第一个数字 0 没有被分配,选择 0;
- s2 的 permutation 中的第一个数字 3 已经被分配了,往后遍历到数字 4,选择 4;
- s0 在 permutation 中往后遍历,0 和 4 都已经被分配了,选择 1;
- s1 在 permutation 中往后遍历,选择 2;
- s2 在 permutation 中往后遍历,4 已经被分配了,选择 5;
- s0 在 permutation 中往后遍历直到选择 6;
于是就有了 lookup table:
| m | slot |
|---|---|
| 0 | s1 |
| 1 | s0 |
| 2 | s1 |
| 3 | s0 |
| 4 | s2 |
| 5 | s2 |
| 6 | s0 |
这种方法类似于开放寻址法中的双重哈希,通过使用两个无关的哈希函数来生成排列(也可以使用其他生成随机排列的方法,例如 fisher-yates shuffle,必须保证方法的的随机性)降低了哈希碰撞的概率;在增加或移除 slot 时,需要为新的 slot 生成 permutation table,再重新生成 lookup table,这会导致部分重新映射,不满足最小化重新映射(minimum disruption);维护两个表的空间复杂度是 O(n),查询的时间复杂度是 O(1);建立表的复杂度可以参考论文的第 3.4 节。

4 总结
本文主要介绍了负载均衡的概念,并简单地阐明了一致性哈希算法的原理,关于一致性哈希算法的优缺点、边界条件、复杂度分析、效率对比、实际应用等还需要结合论文和开源组件进行更深入的了解。