启发式搜索和强化学习

The Pac-Man Projects 是 UC Berkeley CS 188 的课程项目，本文以该项目为例介绍启发式搜索和强化学习。

1 盲目搜索

盲目搜索（Blind Search）指不利用任何额外信息（输入数据，或辅助函数），只依赖于算法本身的搜索，例如 BFS，DFS，Dijkstra 等；

DFS

The Pac-Man Projects 已经实现了吃豆人游戏的后台逻辑和图形渲染框架，我们只需要在 search.py 文件中实现具体的搜索算法，并根据搜索算法生成寻路路径，即可让吃豆人移动，先来实现一个简单的 DFS：

def DepthFirstSearch(problem):
    from util import Stack
    open_list = Stack()
    visited = []
    open_list.push((problem.getStartState(), []))
    while not open_list.isEmpty():
        current_node, path = open_list.pop()
        if problem.isGoalState(current_node):
            return path
        if current_node in visited:
            continue
        visited.append(current_node)
        for next_node, action, cost in problem.getSuccessors(current_node):
            if next_node not in visited:
                open_list.push((next_node, path + [action]))
dfs = DepthFirstSearch

在吃豆人游戏的框架下，为寻路函数传入的 problem 参数可以理解为一个 class SearchProblem 类型的抽象基类，实际的问题有 PositionSearchProblem（找到单个终点），FoodSearchProblem（找到所有食物），CapsuleSearchProblem（找到增益药丸和所有食物）等，这些子类都需要实现以下函数：

  • getStartState()：获取起始状态；
  • isGoalState(state)：判断 state 节点是否是目标节点；
  • getSuccessors(statu)：获取 state 节点的所有后续节点；
  • getCostOfActions(actions)：actions 是一个由上下左右方向组成的一个动作列表，函数返回这个列表的总花费（cost）；

运行一下看看 DFS 的效果：

$ python pacman.py -l smallEmpty -z 0.8 -p SearchAgent -a fn=dfs     
[SearchAgent] using function dfs
[SearchAgent] using problem type PositionSearchProblem
Path found with total cost of 56 in 0.002992 seconds
Search nodes expanded: 56
Pacman emerges victorious! Score: 454
Average Score: 454.0
Scores:        454.0
Win Rate:      1/1 (1.00)
Record:        Win

运行的参数列表中有几个参数：

  • -l smallEmpty：在名为 smallEmpty 的地图上运行，地图定义在 layouts 目录下；
  • -z 0.8：客户端表现缩放为 0.8 倍
  • -p SearchAgent：指定实际的问题，这里的 SearchAgent 是 fn='depthFirstSearch', prob='PositionSearchProblem' 的缩写；

实际运行效果如下：

smallempty-dfs

可以看到吃豆人 agent 绕了很远的路才到达终点，因为 DFS 在计算复杂性理论中是不完备（complete）且非最优（optimality）的。

BFS

def BreadthFirstSearch(problem):
    from util import Queue
    open_list = Queue()
    visited = set()
    open_list.push((problem.getStartState(), []))
    while not open_list.isEmpty():
        current_node, path = open_list.pop()
        if problem.isGoalState(current_node):
            return path
        if current_node in visited:
            continue
        visited.add(current_node)
        for next_node, action, cost in problem.getSuccessors(current_node):
            if next_node not in visited:
                open_list.push((next_node, path + [action]))
bfs = BreadthFirstSearch

BFS 的运行效果如下：

$ python pacman.py -l smallEmpty -z 0.8 -p SearchAgent -a fn=bfs
[SearchAgent] using function bfs
[SearchAgent] using problem type PositionSearchProblem
Path found with total cost of 14 in 0.001995 seconds
Search nodes expanded: 63
Pacman emerges victorious! Score: 496
Average Score: 496.0
Scores:        496.0
Win Rate:      1/1 (1.00)
Record:        Win

smallempty-bfs

可以看到使用 BFS 的 agent 通过最短路径到达了终点，因为 BFS 是完备且最优的。

IDS 的思路是重复进行限制层数的 DFS 来找到最优解，它综合了 DFS 的优点（空间复杂度）和 BFS 的优点（完备且最优），但是在时间复杂度上表现比较差（可以参考输出结果中的 Search nodes expanded）：

def IterativeDeepeningSearch(problem):
    import sys
    from util import Stack

    def depthLimitSearch(problem, depth):
        visited = []
        open_list = Stack()
        open_list.push((problem.getStartState(), [], visited))
        while not open_list.isEmpty():
            current_node, path, visited = open_list.pop()
            if problem.isGoalState(current_node):
                return path
            if len(path) == depth or depth == 0:
                continue
            if current_node in visited:
                continue
            actions = problem.getSuccessors(current_node)
            for next_node, action, cost in actions:
                if next_node not in visited:
                    open_list.push((next_node, path + [action], visited+[current_node]))

    for depth in range(sys.maxsize**10):
        path = depthLimitSearch(problem, depth)
        if path:
            return path
            
ids = IterativeDeepeningSearch

这个算法对于只有小面积可搜索空间的地图效果比较好：

$ python pacman.py -l smallMaze -z 0.8 -p SearchAgent -a fn=ids
[SearchAgent] using function ids
[SearchAgent] using problem type PositionSearchProblem
Path found with total cost of 19 in 0.008976 seconds
Search nodes expanded: 923
Pacman emerges victorious! Score: 491
Average Score: 491.0
Scores:        491.0
Win Rate:      1/1 (1.00)
Record:        Win

smallmaze-ids

但是对于拥有大面积可搜索空间的地图，搜索时间会非常长：

$ python pacman.py -l smallEmpty -z 0.8 -p SearchAgent -a fn=ids
[SearchAgent] using function ids
[SearchAgent] using problem type PositionSearchProblem
Path found with total cost of 14 in 0.710854 seconds
Search nodes expanded: 94552
Pacman emerges victorious! Score: 496
Average Score: 496.0
Scores:        496.0
Win Rate:      1/1 (1.00)
Record:        Win

smallempty-ids

UCS 和 Dijkstra 类似，用一个小根堆保存当前节点到起始节点的距离，依次展开路径花费最小的节点，直到找到终点为止，而一般来说 Dijkstra 没有一个固定的终点：

def UniformCostSearch(problem):
    from util import PriorityQueue
    frontier = PriorityQueue()
    visited = []
    frontier.push((problem.getStartState(), [], 0), 0)
    while not frontier.isEmpty():
        current_node, path, current_cost = frontier.pop()
        if problem.isGoalState(current_node):
            return path
        if current_node in visited:
            continue
        visited.append(current_node)
        for next_node, action, cost in problem.getSuccessors(current_node):
            if next_node not in visited:
                frontier.push((next_node, path + [action], current_cost + cost), current_cost + cost)
ucs = UniformCostSearch

$ python pacman.py -l smallEmpty -z 0.8 -p SearchAgent -a fn=ucs
[SearchAgent] using function ucs
[SearchAgent] using problem type PositionSearchProblem
Path found with total cost of 14 in 0.002992 seconds
Search nodes expanded: 63
Pacman emerges victorious! Score: 496
Average Score: 496.0
Scores:        496.0
Win Rate:      1/1 (1.00)
Record:        Win

smallempty-ucs

2 启发式搜索

传统的盲目搜索算法因为受制于完备性、最优性、时间、空间复杂度等因素，在实际的应用中很少被使用；而在路径规划，最优化算法和人工智能领域，使用启发式搜索（Heuristic Search）能够更好地在准确性和计算速度之间取得平衡。

启发式搜索 Heuristic Search 又叫做有信息搜索 Informed Search，启发式搜索不同于盲目搜索的地方有两点：一是启发式搜索依赖于启发函数，启发函数 Heuristic Function 是用于估计当前节点到目标节点距离的一类函数；二是它需要利用输入数据并将其作为启发函数的参数，以衡量当前位置到目标位置的距离关系。

启发式搜索通过衡量当前位置到目标位置的距离关系，使得搜索过程的移动方向优先朝向目标位置更近的方向前进，以提高搜索效率。

启发函数

启发函数 h(n) 用于给出从特定节点到目标节点的距离的估计值（而不是真实值）；许多寻路问题都是 NP 完备（NP-completeness）的，因此在最坏情况下它们的算法时间复杂度都是指数级的；找到一个好的启发函数可以更高效地得到一个更优的解；启发函数算法的优劣直接决定了启发式搜索的效率。

最简单的启发函数有：

  • null heuristic：估计值始终等于 0，相当于退化成了 UCS（只计算当前节点到起始节点的距离）；
  • 曼哈顿距离：两点在南北方向上的距离加上在东西方向上的距离，即 abs(a − x) + abs(b − y)；
  • 欧几里得距离：两点在欧氏空间中的直线距离，即 sqrt((a - x) ^ 2 + (b - y) ^ 2)；

A*

A* 是一种应用很广泛的启发式搜索算法，其主要思路与 Dijkstra 和 UCS 类似，都是利用一个小根堆，不断地取出堆顶节点并判断其是否是目标节点，不同的是它会为每一个已知节点计算出从起点和终点的距离之和 f(x) = g(x) + h(x)，其中 g(x) 是从起点到当前节点的实际距离，h(x) 是使用启发函数计算得到的从当前节点到目标节点的估计距离：

def AStarSearch(problem, heuristic=nullHeuristic):
    from util import PriorityQueueWithFunction
    def AStarHeuristic(item):
        state, _, cost = item
        h = heuristic(state, problem=problem)
        g = cost
        return g + h

    frontier = PriorityQueueWithFunction(AStarHeuristic)
    visited = []

    frontier.push((problem.getStartState(),[], 0))
    while not frontier.isEmpty():
        currentNode, path, currentCost = frontier.pop()
        if problem.isGoalState(currentNode):
            return path
        if currentNode not in visited:
            visited.append(currentNode)
            for nextNode, action, cost in problem.getSuccessors(currentNode):
                if nextNode not in visited:
                    frontier.push((nextNode, path + [action], currentCost + cost))

astar = AStarSearch

对于多节点的搜索问题，需要综合考虑所有目标节点对于当前节点的影响；我们可以利用贪心的思想，让吃豆人优先靠近距离较近的豆子，也就是使得距离当前节点更近的目标节点的启发函数值更小，这样距离吃豆人更近的豆子就会更有可能具有更小的 f(x) 值；在为启发函数传入的参数中， state 是一个包含当前位置 position 和所有目标点信息结构 grid 的二元组，可以使用 grid.asList() 将所有目标点转换为一个数组：

def FoodHeuristic(state, problem):
    position, food_grid = state
    food_gridList = food_grid if isinstance(food_grid, list) else food_grid.asList()
    from util import manhattanDistance
    minx, miny = position
    maxx, maxy = position
    for food in food_gridList:
        foodx, foody = food
        minx = min(foodx,minx)
        maxx = max(foodx,maxx)
        miny = min(foody,miny)
        maxy = max(foody,maxy)
    return abs(minx-maxx) + abs(miny-maxy)

$ python pacman.py -l tinySearch -p SearchAgent -a fn=astar,prob=FoodSearchProblem,heuristic=FoodHeuristic
[SearchAgent] using function astar and heuristic foodHeuristic
[SearchAgent] using problem type FoodSearchProblem
Path found with total cost of 27 in 0.294214 seconds
Search nodes expanded: 1544
Pacman emerges victorious! Score: 573
Average Score: 573.0
Scores:        573.0
Win Rate:      1/1 (1.00)
Record:        Win

tinySearch-astar

换个地图看看效果：

$ python pacman.py -l mediumDottedMaze -p SearchAgent -a fn=astar,prob=FoodSearchProblem,heuristic=FoodHeuristic
[SearchAgent] using function astar and heuristic foodHeuristic
[SearchAgent] using problem type FoodSearchProblem
Path found with total cost of 74 in 0.091756 seconds
Search nodes expanded: 389
Pacman emerges victorious! Score: 646
Average Score: 646.0
Scores:        646.0
Win Rate:      1/1 (1.00)
Record:        Win

mediumdottedmaze-astar

相比之下，如果使用 nullHeuristic（退化为 UCS）的话搜索花费的时间则会长很多：

$ python pacman.py -l tinySearch -p SearchAgent -a fn=ucs,prob=FoodSearchProblem
[SearchAgent] using function ucs
[SearchAgent] using problem type FoodSearchProblem
Path found with total cost of 27 in 2.880744 seconds
Search nodes expanded: 5057
Pacman emerges victorious! Score: 573
Average Score: 573.0
Scores:        573.0
Win Rate:      1/1 (1.00)
Record:        Win

tinySearch-astar-null-heuristic

3 强化学习

强化学习

强化学习是指通过与环境进行交互和反馈来学习一种策略的过程，在这个过程中，一个强化学习的实体 agent 通过与环境 Environment 进行交互并采取一系列行为 Action 来获得一定的收益 Reward，从而更新采取相应行为的权重。

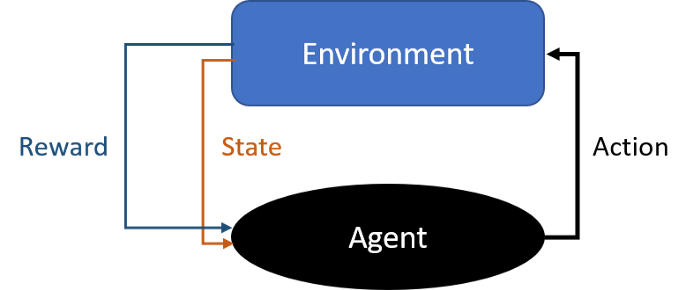
reinforcement-learning-process

强化学习的目标是通过学习得到某个策略 Policy，使得 agent 从 environment 中获得的长期收益最大化，因此在一般的问题中，在没有达到最终的目的前，reward 通常都是负数（随时间的增加而减少），而仅在达到最终的目的时获得较大的正反馈，这样的学习任务通常称为 episodic task（例如吃豆人游戏中的单节点搜索问题）；在另一类问题中，可能需要完成多个目标才能到达最终状态，其 reward 离散地分布在一个连续的空间中，这一类任务称为 continuing task（例如吃豆人游戏中的多节点搜索问题），对于 continuing task，我们可以定义其 reward 为：

discounted-reward

其中 γ 是衰减率（discount factor），衰减率可以使得我们更加偏好近期收益；引入衰减系数的理由有很多，例如避免陷入无限循环，降低远期利益的不确定性，最大化近期利益，利用近期利益产生新的利益因而其更有价值等等。

而强化学习的结果是就是 Gt，通过 argmax 取得的值能够给出在每个状态下我们应该采取的行动，我们可以把这个策略记做 π(a|s)，它表示在状态 s 下采取行动 a 的概率。

马尔科夫决策过程

马尔科夫决策过程（Markov Decision Process, MDP）是指在每个状态下，agent 对于行动 a 的选取只依赖于当前的状态，与任何之前的行为都没有关系；几乎所有的强化学习问题都可以使用 MDP 解决，一个标准的马尔可夫决策过程由一个四元组组成：

  • S：State，状态空间的集合，S0 表示初始状态；
  • A：Action，行为空间的集合，包含每个状态可以进行的动作；
  • r(s’ | s, a)：Reward，在 s 状态下，进行 a 操作并转移到 s‘ 状态下的奖励；
  • P(s’ | s, a)：Probability，在 s 状态下，进行 a 操作并转移到 s‘ 状态下的概率；

求解 MDP 问题的常见方法有 Value iteration，Policy iteration，Q-Learning，Deep Q-Learning Network 等等。

Value Iteration

Value Iteration 是一种基于模型的（model-based）算法，使用 Value Iteration 来解决 MDP 问题的前提是我们知道关于模型的所有信息，即 MDP 四元组的所有内容。

假设现在有一个 3*4 叫做 GridWorld 的地图如图所示，以左下角格子为 (0, 0) 原点，其中 (1, 1) 为不可通过的墙，(2, 3) 为奖励为 +1 的终点，(1, 3) 为 -1 的终点；我们定义每一个位置的价值为 V(state)，即对于 state(x, y)，V(state) 表示其能获取的最大价值；每一个位置初始化时其 value 均为 0：

value-iteration-0

在迭代过程中，使用贝尔曼方程（Bellman Equation）更新所有位置的 value，它描述了最佳策略必须满足的条件，前半部分 r(s, a, s’) 代表采取了 a 行为之后得到的 reward，后半部分；我们需要在每轮迭代中计算每个状态的价值即 V(s)，直到两次迭代结果的差值小于给定的阈值才能认为其收敛了，这里的 V(s) 也叫做 q-value：

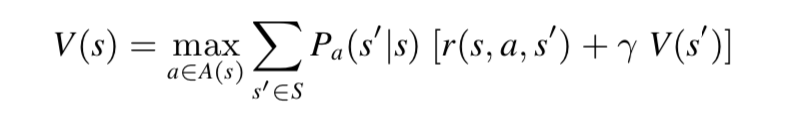
bellman-equation

经过前三次迭代分别得到：

value-iteration-1

value-iteration-2

value-iteration-3

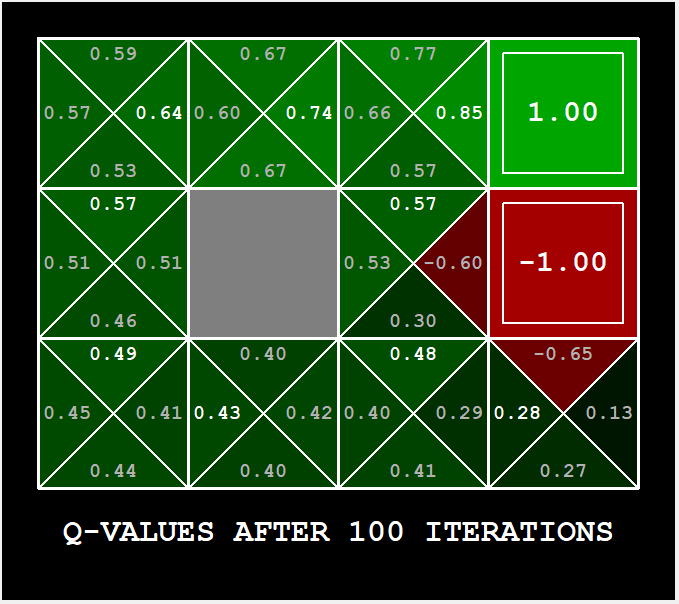
收敛速度是指数级，并且随着迭代的不断进行，终将得到最优的 V(s)；或者说当迭代次数趋近于无穷大的时候，将得到 V(s) 的最优解；经过 100 次迭代后将得到：

value-iteration-100

取 argmax 即可得到最优的策略（即上图中的小箭头）；也可以看到采取每一种行动对应的 Probaility：

value-iteration-100-argmax

进行 Value Iteration 的流程主要对应 runValueIteration 和 computeQValueFromValues 两个函数，迭代结束后选择策略则对应 computeActionFromValues 函数：

# valueIterationAgents.py

class ValueIterationAgent(ValueEstimationAgent):
    """
        A ValueIterationAgent takes a Markov decision process
        (see mdp.py) on initialization and runs value iteration
        for a given number of iterations using the supplied
        discount factor.
    """
    def __init__(self, mdp, discount = 0.9, iterations = 100):
        """
          Some useful mdp methods you will use:
              mdp.getStates()
              mdp.getPossibleActions(state)
              mdp.getTransitionStatesAndProbs(state, action)
              mdp.getReward(state, action, nextState)
              mdp.isTerminal(state)
        """
        self.mdp = mdp
        self.discount = discount
        self.iterations = iterations
        self.values = util.Counter() # A Counter is a dict with default 0
        self.runValueIteration()

    def runValueIteration(self):
        for _ in np.arange(0, self.iterations):
            next_values = util.Counter()

            for state in self.mdp.getStates():
                if self.mdp.isTerminal(state):
                    continue

                q_values = util.Counter()

                for action in self.mdp.getPossibleActions(state):
                    q_values[action] = self.computeQValueFromValues(state, action)

                key_max_value = q_values.argMax()
                next_values[state] = q_values[key_max_value]

            self.values = next_values

    def getValue(self, state):
        return self.values[state]


    def computeQValueFromValues(self, state, action):
        """
          Compute the Q-value of action in state from the
          value function stored in self.values.
        """
        next_states_probs = self.mdp.getTransitionStatesAndProbs(state, action)
        q_value = 0

        for (next_state, next_state_prob) in next_states_probs:
            q_value += next_state_prob * (self.mdp.getReward(state, action, next_state) + self.discount * self.values[next_state])

        return q_value
    
    def computeActionFromValues(self, state):
        """
          The policy is the best action in the given state
          according to the values currently stored in self.values.

          You may break ties any way you see fit.  Note that if
          there are no legal actions, which is the case at the
          terminal state, you should return None.
        """
        if self.mdp.isTerminal(state):
            return None

        actions = self.mdp.getPossibleActions(state)
        values = util.Counter()

        for action in actions:
            values[action] = self.computeQValueFromValues(state, action)

        policy = values.argMax()
        return policy


    def getPolicy(self, state):
        return self.computeActionFromValues(state)

    def getAction(self, state):
        "Returns the policy at the state (no exploration)."
        return self.computeActionFromValues(state)

    def getQValue(self, state, action):
        return self.computeQValueFromValues(state, action)

Q-Learning

Q-Learning 的思路与 Value Iteration 有一些类似，但它是一种模型无关的（model-free）算法，使用 Q-Learning 的时候我们的 agent 无需事先知道当前环境中的 State，Action 等 MDP 四元组内容，

在使用 Value Ietration 的时候，我们需要在每一个 episode 对所有的 State 和 Action 进行更新，但在实际问题中 State 的数量可能非常多以致于我们不可能遍历完所有的状态，这时候我们可以借助 Q-Learning，在对于环境未知的前提下，不断地与环境进行交互和探索，计算出有限的环境样本中 Q-Value，并维护一个 Q-Table：

Sr(s’ | s, action 1)r(s’ | s, action 2)…
S1 (0, 0)3-1
S2 (0, 1)-24
…

在刚开始时，agent 对于环境一无所知，因此 Q-Table 应该被初始化为一个零矩阵；当我们处于某个状态 s （例如表里的 S1）时，根据 Q-Table 中当前的最优值和一定的策略（Multi-armed bandit 问题，利用 ε-greedy，UCB 等解决）选择对应的动作 a （假设选择了表里的 action 1，对应 r = 3）进行探索，并根据获得的即时奖励 r 来更新奖励，这里的 r 只是即时获得的奖励（r = 3），因为还要考虑所转移到的状态 s’ （表里的 S2）在未来可能会获取到的最大奖励（r’ = 4）；

q-learning-paper

真正的奖励 Q(St, At) 由公式中的两部分组成，前半部分 r 是通过动作 a 即时获得的奖励（r = 3），后半部分 γ * max(a’)Q(s’, a’) 是对未来行为的最大期望奖励（r’ = 4），且后半部分往往是不确定的，因此需要乘以衰减率 γ：

q-function

在通过计算得到当前行为所能获得的预期奖励后，将其减去表中对当前环境的估计奖励 Q(s,a)（r = 3），再乘以学习率，就能用来更新 Q-Table 中的值了。

agent 不断地与环境进行探索并发生状态转换，直到到达目标；我们将 agent 的每一轮探索（从任意起始状态出发，经历若干个 action，直到到达目标状态）称为一个 episode；在进行指定 episode 次数的训练之后，取 argmax 得到的策略就是当前的最优解。

现在利用 epsilon-greedy 作为探索策略，训练 10 个 episode：

$ python gridworld.py -a q -k 10 --noise 0.0 -e 0.9

q-learning-epsilon-greedy-10-episodes

得到结果之后，对每一个状态 s 的所有动作 a 取 argmax 即可得到在当前 epsilon 值和 episode 值下的最优解：

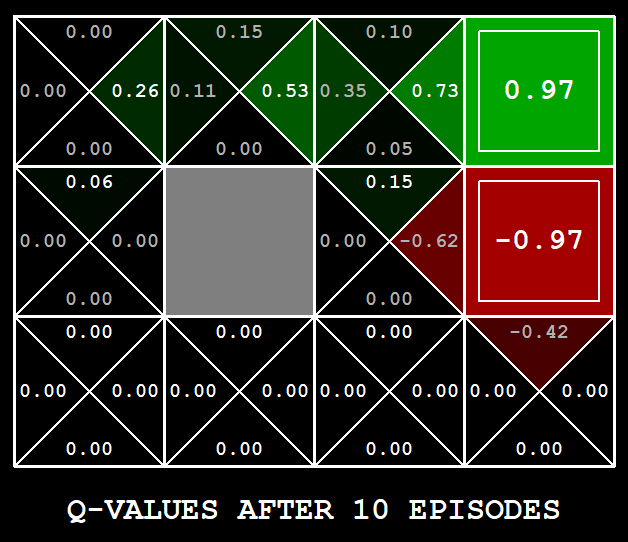
q-learning-epsilon-greedy-10-episodes

Q-Learning 的实现大致如下：

class QLearningAgent(ReinforcementAgent):
    def __init__(self, **args):
        ReinforcementAgent.__init__(self, **args)
        self.q_values = defaultdict(lambda: 0.0)

    def getQValue(self, state, action):
        """
          Returns Q(state,action)
          Should return 0.0 if we have never seen a state
          or the Q node value otherwise
        """
        return self.q_values[(state, action)]

    def computeValueFromQValues(self, state):
        """
          Returns max_action Q(state,action)
          where the max is over legal actions.  Note that if
          there are no legal actions, which is the case at the
          terminal state, you should return a value of 0.0.
        """
        next_actions = self.getLegalActions(state)

        if not next_actions:
            return 0.0
        else:
            q_value_actions = [(self.getQValue(state, action), action) for action in next_actions]
            # return the max in q_value_actions which is q_value
            return sorted(q_value_actions, key=lambda x: x[0])[-1][0]

    def computeActionFromQValues(self, state):
        """
          Compute the best action to take in a state.  Note that if there
          are no legal actions, which is the case at the terminal state,
          you should return None.
        """
        next_actions = self.getLegalActions(state)

        if not next_actions:
            return None
        else:
            actions = []
            max_q_value = self.getQValue(state, next_actions[0])

            # find actions with max q value
            for action in next_actions:
                action_q_value = self.getQValue(state, action)
                if max_q_value < action_q_value:
                    max_q_value = action_q_value
                    actions = [action]
                elif max_q_value == action_q_value:
                    actions.append(action)

            # break ties randomly for better behavior. The random.choice() function will help.
            return random.choice(actions)

    def getAction(self, state):
        """
          Compute the action to take in the current state.  With
          probability self.epsilon, we should take a random action and
          take the best policy action otherwise.  Note that if there are
          no legal actions, which is the case at the terminal state, you
          should choose None as the action.
        """
        # Pick Action
        legalActions = self.getLegalActions(state)
        action = None
        if legalActions:
            if util.flipCoin(self.epsilon):
                return random.choice(legalActions)
            else:
                action = self.getPolicy(state)

        return action

    def update(self, state, action, nextState, reward):
        """
          The parent class calls this to observe a
          state = action => nextState and reward transition.
          You should do your Q-Value update here

          NOTE: You should never call this function,
          it will be called on your behalf
        """
        state_action_q_value = self.getQValue(state, action)
        self.q_values[(state, action)] = state_action_q_value + self.alpha * (reward + self.discount * self.getValue(nextState) - state_action_q_value)

    def getPolicy(self, state):
        return self.computeActionFromQValues(sta、te)

    def getValue(self, state):
        return self.computeValueFromQValues(state)

DQN

Q-Learning 依赖于 Q-Table，其存在的问题是当 Q-Table 中的状态非常多，或状态的维度非常多的时候，内存可能无法存储所有的状态，此时我们可以利用神经网络来拟合整个 Q-Table，即使用 Deep Q-Learning Network。DQN 主要用来解决拥有近乎无限的 State，但 Action 有限的问题，它将当前 State 作为输入，输出各个 Action 的 Q-Value。

deep-q-learning-network

启发式搜索和强化学习的对比

pacman-contest